- Représentation Graphique des Paragenèses des Métabasites et des Métapélites - english version

Des représentations graphiques sont proposées pour représenter les paragenèses des roches métamorphiques les plus communes. Ainsi le diagramme ACF est utilisé pour représenter les paragenèses des roches magmatiques basiques (métabasalte, métagabbro), les métabasites. Les diagrammes A'KF et AFM sont utilisés pour représenter les paragenèses des roches pélitiques, les métapélites.

Une amphibolite (à gauche) et une métapélite (à droite) ont des paragenèses différentes bien que les 2 roches aient recristallisé dans des conditions P T identiques : celles du faciès amphibolite. (microphotographies en LPNA)

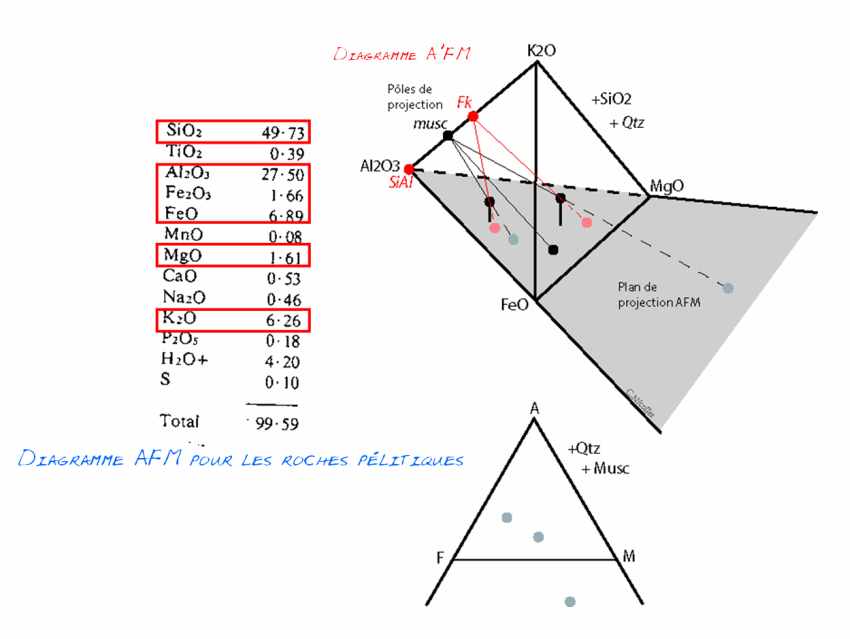
Les Paragenèses des Métabasites : Il est rare que seulement 3 constituants chimiques (dont les variations sont représentables dans un triangle ; voir exemple précédent) rendent compte de la composition d'un roche. Voici la composition d'une métabasite ; onze éléments ont des concentrations non négligeables. On en retiendra 5 qui totalisent près de 95%. Ce sont SiO2, Al2O3, FeO, MgO, CaO. Pour simplifier, nous négligeons les autres.

Le tétraèdre A(Al2O3) - C(CaO) - F(FeO+MgO)- S(SiO2) est représentatif de la composition des roches magmatiques basiques. Quelques minéraux de ces roches sont portés sur la figure : Qtz pour le quartz, Opx pour orthopyroxène, Cpx pour clinopyroxène, Pl pour plagioclase, Grt pour grenat et Spl pour spinelle. Les lignes de liaisons entre ces différents minéraux permettent de définir des paragenèses à 4 minéraux. Sur la figure de gauche, Qtz-Opx-Grt-Pl ; Qtz-Cpx-Opx-Pl ; Opx-Cpx-Pl-Grt ; Spl-Opx-Grt-Cpx ; Spl-Cpx-Grt-Pl (les lignes de liaisons faisant intervenir le Spl ne sont pas représentées pour plus de clarté, à moins d'utiliser la visualisation 3D). Sur la figure de droite, Qtz-Opx-Grt-Cpx ; Qtz-Cpx-Grt-Pl ; Opx-Cpx-Pl-Grt ; Spl-Opx-Grt-Cpx ; Spl-Cpx-Grt-Pl. Les 2 figures correspondent à des conditions métamorphiques différentes. Celles-ci ne sont pas très faciles à lire. Aussi, on préfére utiliser une projection de ce tétraèdre, à partir de son sommet S (où se trouve le Qtz), sur sa base : le triangle ACF. Une solution bien pratique est la visualisation en 3D !

Il est cependant difficile de représenter graphiquement les variations de 5 constituants. Il est donc nécessaire de diminuer ce chiffre. La première solution est de considérer FeO et MgO comme un seul constituant (Fe+Mg)O. En effet, l'ajout du constituant FeO (ou MgO) à un système purement magnésien (ou férifère) n'augmente pas le nombre de minéraux (comme l'indique la règle des phases) : si l'on ajoute du fer à une forstérite (olivine magnésienne), on ne fabrique pas deux minéraux, mais une olivine "solution solide ferro-magnésienne". Il reste 4 constituants dont on peut représenter les variations dans un tétraèdre. Cependant, il s'agit d'une figure encore difficile à visualiser sur l'espace en 2 dimensions d'une feuille de papier. La solution est de projeter le volume de ce tétraèdre sur un triangle. Mais la règle des phases nous indique que 4 minéraux constituent la paragenèse (=assemblage divariant avec M=C) des roches à représenter dans ces figures, ce qui est impossible sans faire croiser des lignes de liaison. La solution consiste à choisir un des minéraux de la paragenèse comme pôle de projection. Dans le cas du triangle ACF utilisé pour représenter les roches basiques, le Quartz est le pôle de projection. C'est pourquoi, ce minéral doit faire partie de la paragenèse des roches représentées dans ce diagramme. On rappelle cette condition en écrivant Q à côté du diagramme.

Le diagramme triangulaire A(Al2O3) - C(CaO) - F(FeO+MgO) est une projection du tétraèdre S(SiO2)ACF depuis le sommet S où se trouve le quartz (Q). Pour plus de clarté, seules les paragenèses contenant le Q sont représentées. A titre d'exemple, j'ai dessiné la paragenèse O-C-P-G de la figure précédente : la ligne jointive en pointillé CG est "caché" par les plans O-C-P et O-G-P.
Les 2 triangles correspondent respectivement aux faciès granulite de Basses P et de P Intermédiaires. On passe de l'une à l'autre en remplacant la ligne de liaison O-P par la ligne C-G ; on franchit l'équilibre univariant Opx + Pl = Cpx + Gt + Q.

Sur ce triangle, les triangles Opx-Gt-Pl et Opx-Cpx-Pl représentent respectivement les paragenèses Opx-Gt-Pl-Q et Opx-Cpx-Pl-Q. Par contre, on ne peut représenter les paragenèses sans Q de la partie inférieure du tétraèdre sans rendre la figure difficilement lisible. On s'impose donc de ne représenter que les paragenèses à Q. De ce fait, cette projection est extrêmement restrictive, car elle rend impossible la représentation de l'important volume inférieur du tétraèdre SiO2-Al2O3-" F "-CaO, sous les plans Opx-Cpx-Pl et Opx-Gt-Pl, cad les roches basiques sous saturées en silice et roches ultrabasiques. Pour de telles roches, il est toujours possible de changer les paramètres de la projection. On choisit par exemple comme plan de projection, le plan SCF et comme pôle de projection le corindon ou le spinelle, sous réserve que ces minéraux soient présents dans les roches étudiées. La visualisation 3D est aussi un outil de travail confortable !

Les Paragenèses des Métapélites : Le même raisonnement que précédemment permet de retenir 5 éléments majeurs de l'analyse de la métapélite du tableau ci dessous. Il s'agit de SiO2, Al2O3, FeO, MgO, K2O. Le diagramme A'KF est une projection du tétraèdre SiO2-Al2O3-" F "-K2O sur le triangle AKF à partir du pôle de projection SiO2. Comme pour le diagramme ACF, fer et magnésium sont considérés comme un seul élément.

Dans le diagramme AFM, fer et magnésium sont considérés au contraire comme deux constituants indépendants. Comme le quartz est un minéral omniprésent et abondant dans les métapélites, on admet que la silice est en excès et on fait abstraction de cet élément dans le calcul, sous réserve de ne représenter que des roches contenant du quartz. Les quatre éléments restant Al2O3- FeO-MgO-K2O sont représentés dans un tétraèdre pour lequel il faut définir une surface et un pôle de projection coïncidant avec un minéral. La base du tétraèdre AFM sert de plan de projection ; il n'y a pas de minéral commun des métapélites au pôle opposé : K2O ( en fait, K2SiO3, puisque la silice est en excès). La muscovite, sur la ligne A-K est, par contre, un minéral commun. Le diagramme AFM est utilisée pour représenter des paragenèses à Q et Musc. On remarque que les côtés AF et AM du triangle AFM se prolongent au delà de F et M respectivement : ceci est lié au fait que le pôle de projection " muscovite " est " bas " dans le tétraèdre. De ce fait, quelques minéraux (eg biotite) et roches peu potassiques et peu alumineux sont projetés en dehors du triangle. Ce petit problème géométrique n'a pas de conséquence sur l'interprétation pétrologique. Voir le tétraèdre AFMK en 3D ?

Dans les conditions des faciès amphibolite profond et granulite, la muscovite est instable (en présence de Q) et est remplacée par un autre minéral potassique : le feldspath potassique par le biais de la réaction Musc + Q = SiAl + FK + V (SiAl : silicate d'alumine). Au delà de cette réaction, la projection est faite depuis le feldspath potassique qui se trouve aussi sur la ligne A-K. Ce minéral est plus proche du pôle K que ne l'est la muscovite ; en conséquence, plus aucun minéral et roche ne sont projetés à l'extérieur du triangle que l'on appelle A'FM (pour le différencier du triangle AFM). Voir le tétraèdre AFMK en 3D ?

Voir les diagrammes AFM d'un gradient métamorphique de MP-HT.

Retour au Cours de Métamorphisme, de Pétrologie Endogène , à la Photothèque ou bien à la première page ?