METAMOD : un logiciel de modélisation des trajectoires Pression - Température - temps (P - T - t) des roches métamorphiques
NICOLLET Christian et BERNARD Maurice
L'histoire de la Terre, est conditionnée, depuis sa genèse, par son évolution thermique. C'est l’énergie thermique qui fait fonctionner la machine Terre. Volcanisme et flux de chaleur sont des exemples manifestes de l'énergie thermique, interne du globe : ils résultent des transferts de la chaleur, des profondeurs du globe vers la surface, associés au lent refroidissement de notre planète. De même, la tectonique des plaques est liée à de vastes mouvements de convection dans le manteau dont le moteur est l'énergie thermique.
Pour nous renseigner sur la situation thermique de la lithosphère à différents moments de son histoire, il nous faut trouver des "fossiles", des traceurs qui ont d'enregistré les variations thermiques et qui sont donc capables de nous renseigner sur elles. Les roches métamorphiques représentent de tels témoins.
LES ROCHES METAMORPHIQUES : TEMOINS DE L’EVOLUTION
THERMIQUE DE LA LITHOSPHERE
![]()
Gradient métamorphique et trajets P, T, t des roches au cours d’une orogenèse :
A l'intérieur du globe, la température (T) augmente avec la profondeur. Dans la partie superficielle de la croûte continentale, la T augmente de 3° tous les 100 m. Cette augmentation de la température avec la profondeur (Z) peut être représentée par une courbe T = f(Z), exprimée en °/km, que l'on appelle le géotherme (Gm sur la fig. 1b). Celui-ci varie significativement dans l'espace et dans le temps (t).
Le cas le plus spectaculaire de variations thermiques au cours du temps s’observe lors de la convergence de deux continents qui, en provoquant un redoublement de la croûte continentale, est à l’origine des chaînes de montagnes. La figure 1a schématise l'épaississement et l’amincissement de la croûte continentale impliquée dans un mouvement de convergence. La fig. 1b montre, elle, les trajectoires PTt des roches R et l’évolution des géothermes au cours du temps (Gm, t0, t1, ...). Au cours de l'épaississement, une roche (R1), initialement à la surface d'une croûte d'épaisseur "normale", chevauchée, se réchauffe lentement tandis qu'elle s'enfonce. Dans le diagramme PT, elle suit un trajet proche de l'axe des pressions (P), qualifié de HP-BT. Lorsque la convergence s'interrompt, la croûte épaissie est en déséquilibre gravitaire et aura tendance à s'amincir. L'échantillon va remonter vers la surface (P diminue), mais continue, dans un premier temps, de se réchauffer. Il se réchauffe au-delà du géotherme " moyen " (Gm, t1, t2, t3). Ensuite seulement, T diminue en même temps que P jusqu'à ce que l'échantillon arrive à la surface où nous pouvons l'échantillonner.
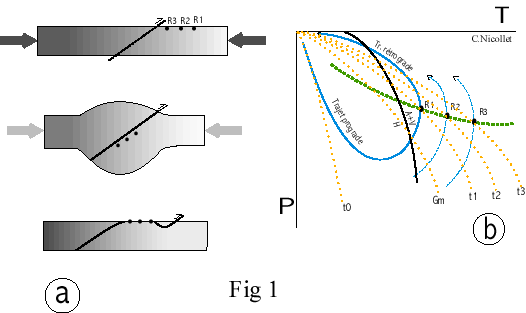
Cette boucle correspond au trajet thermique suivi par une roche. Mais que va enregistrer la roche de ce trajet ? Tout le long de cette évolution thermique, des réactions minéralogiques tenteront de modifier l'association minéralogique de la roche afin que les associations de minéraux soient compatibles avec les conditions P-T du moment. Ces réactions sont généralement des réactions de déshydratation du type :
H = A + V
lorsque T augmente (fig. 1b). H est un assemblage de minéraux hydratés, A de minéraux anhydres et V la phase vapeur (dont la composition est ici H2O). Au cours d'un métamorphisme prograde (T et P augmentent), cette vapeur libérée par la roche, de faible densité, remonte vers la surface. Au cours du métamorphisme rétrograde, lorsque T diminue, de telles réactions sont franchies en sens inverse, mais la vapeur nécessaire à leurs réalisations, n'est plus disponible : l'association minéralogique de plus hautes T persiste. A cela s'ajoute que les réactions sont favorisées par la déformation, laquelle est très localisée au cours de l'évolution rétrograde. Les conditions maximales atteintes par différentes roches, collectées dans une région, matérialisent le gradient métamorphique (en tirets épais sur la fig.1b). Celui-ci ne nous informe que sur un seul point des trajets PTt des différentes roches (fig. 1b). Ce qui est limité ! Dans quelques cas exceptionnels, toutefois, les roches enregistrent d’autres points, des portions de leurs trajets thermiques.
Le but de cet ouvrage est de comprendre et de " modéliser " ces boucles thermiques, les trajets PTt suivis par les roches et la diversité de ces trajets. Pour cela, nous devons, tout d’abord, nous interroger sur les sources de chaleur dans la lithosphère et les modes de transfert de celle-ci.
SOURCES ET DISSIPATION DE LA CHALEUR
DANS LE GLOBE :
![]()
La répartition de la chaleur dans le globe résulte de différentes sources de chaleur et du mode de transfert de cette chaleur à travers le globe. Les sources de chaleur se répartissent à tous les niveaux du globe. Il s’agit principalement de la chaleur initiale, liée à l’accrétion de notre planète à son origine, de la chaleur latente de cristallisation du noyau, de la chaleur produite dans les roches par la désintégration des éléments radioactifs. Ces derniers sont localisés dans le manteau supérieur et surtout dans la croûte continentale. Ils représentent donc une source de chaleur considérable dans celle-ci.
Le transfert de chaleur en fonction du temps, en un point du globe, est exprimé par l’équation différentielle :
![]() (1)
(1)
![]() est l'opérateur
Laplacien : il indique la dérivée seconde de T dans l'espace à 3 dimensions.
est l'opérateur
Laplacien : il indique la dérivée seconde de T dans l'espace à 3 dimensions.
![]() est le gradient (de T). Dans le globe,
les transferts de chaleur se font dans les 3 dimensions.
est le gradient (de T). Dans le globe,
les transferts de chaleur se font dans les 3 dimensions.
Cette équation se simplifie en :
![]() (2)
(2)
si l’on ne considère que les transferts verticaux (à la vitesse u), en fonction de la profondeur z (modèle à une dimension). T est la température, t le temps, ![]() la masse volumique. Cp est la capacité thermique (mesure la chaleur nécessaire pour faire augmenter de un degré la température d’un volume unitaire de roche). A est la production de chaleur libérée par les roches,
la masse volumique. Cp est la capacité thermique (mesure la chaleur nécessaire pour faire augmenter de un degré la température d’un volume unitaire de roche). A est la production de chaleur libérée par les roches, ![]() (kappa) la diffusivité thermique, c’est à dire de la capacité de ces roches à laisser circuler la chaleur.
(kappa) la diffusivité thermique, c’est à dire de la capacité de ces roches à laisser circuler la chaleur.
Cette équation fait apparaître les principaux modes de transfert et de production (ou pertes) de chaleur. Le premier terme de l’équation, la production de chaleur est essentiellement liée à la désintégration des éléments radioactifs dans les roches, qui sont concentrés dans la croûte continentale ; on doit y ajouter la chaleur latente de cristallisation des magmas. Les processus métamorphiques sont, également, sources ou pertes de chaleur selon que les réactions sont endo- ou exothermiques. Le second terme de l’équation quantifie le mode de transfert de chaleur par conduction : il est fonction de la diffusivité thermique des roches (![]() ). Le transfert de chaleur par convection, troisième terme de l’équation, est fonction de la vitesse de déplacement du milieu (u) et du gradient thermique. Le signe - devant le troisième terme de l’équation montre qu’il y a compétition entre les deux modes de transfert de la chaleur.
). Le transfert de chaleur par convection, troisième terme de l’équation, est fonction de la vitesse de déplacement du milieu (u) et du gradient thermique. Le signe - devant le troisième terme de l’équation montre qu’il y a compétition entre les deux modes de transfert de la chaleur.
LE LOGICIEL METAMOD - MODELISATION DES
TRAJETS P - T - t :
![]()
Le logiciel METAMOD va nous permettre de simuler les trajets P, T, t suivis par des roches dans des contextes géodynamiques variés et de comparer ces trajets avec les évolutions métamorphiques des roches. Ainsi, nous comparerons ces simulations à ce qu’on observe au cours du métamorphisme régional dans les chaînes de montagne ; nous essayerons également de comprendre comment se forme le magma à l’origine de la croûte océanique.
Le programme utilisé dans ce logiciel est basé sur une solution analytique de l’équation de la chaleur (2), proposée par Carslaw et Jaeger en 1959 (voir en annexe). Dans ce modèle, les roches se déplacent à vitesse verticale (modèle à une dimension) constante de telle manière que la profondeur z à un temps t est
z(t) = z0 - ut
Le milieu est homogène vers le bas (milieu semi - infini). Cette dernière simplification est très importante, car, de ce fait, le modèle ne prend pas en compte la distinction croûte - manteau dans lesquels les paramètres thermiques sont très différents. Ceci a des conséquences (quantitatives) importantes sur les trajets PTt. Ceci montre les limites de cette modélisation. Mais celle-ci reste, malgré tout, une bonne approche (qualitative) des évolutions thermiques au cours des processus métamorphiques dans la lithosphère.
Installation du programme :
METAMOD fonctionne sur un PC. Deux versions sont proposées, l’une pour Windows 311, l’autre pour Windows 95, 98 et Windows NT. L’installation nécessite de lancer le programme " Instal31.exe" ou " Instal95.exe" depuis la disquette fournie sur le disque dur de votre ordinateur. Dans le répertoire " metamod " ainsi créé, le programme "metamod.exe " permet de lancer la simulation. On peut créer une fenêtre dans le gestionnaire des programmes de Windows 311 (et Windows NT) et un raccourci dans Windows 95 (et 98). Pour plus de précision sur l’installation (et la désinstallation), lire le fichier " lisezmoi.txt " dans la disquette.
La fenêtre principale du programme
:
![]()
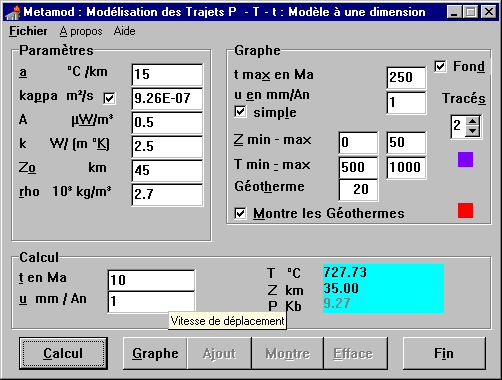
Une fois lancé " metamod.exe " (en double - cliquant sur le raccourci ou sur l’icône correspondante dans le répertoire " metamod "), une fenêtre apparaît, composée de 3 cadres et 6 boutons. A gauche, un cadre " Paramètres ", à droite, un deuxième intitulé " Graphe " et un troisième, en dessous, intitulé " Calcul ". Des petits cadres jaunes d’aide apparaissent lorsque l’on fait glisser lentement la souris (sans cliquer). Une aide en ligne, avec de nombreux liens hypertexte, facilite l’utilisation du programme.
Le premier cadre " Paramètres " fournit les paramètres thermiques et physiques utilisés par le " Calcul " et pour l’élaboration d’un graphe Z (profondeur) = f(T). Ces paramètres sont le gradient géothermique initial (a), exprimé en °C/km. k (kappa) est la diffusivité thermique (m2/s). A est la production (et perte) de chaleur des roches (mW/ m3). k est la conductivité thermique (W/m°K) ; elle varie entre 2 et 5 dans les roches. Z0 est la profondeur initiale choisie pour l’exercice. Elle est de 0 km dans le cas d’un enfouissement (ou épaississement). r (rho) est la masse volumique (2 700 kg /m3 en moyenne dans la croûte continentale).
Les valeurs de ces paramètres sont prédéfinies dans les exercices proposés. Mais on peut choisir d’autres valeurs. La valeur de " a " est inférieure à 30°C/km (valeur dans la partie supérieure de la lithosphère). Pour des exercices simulant l’enfouissement, on choisit une valeur maximale (par ex. 30°/km ; voir exercice 2). Pour des exercices simulant l’exhumation, cette valeur est choisie, en général, en fonction de la température T0 que l’on souhaite donner à la profondeur initiale Z0. A Z0, c’est à dire à t0 (=0), l’équation (3 ; voir en annexe) utilisée par le programme se simplifie en T0 = a . z0 . Pour choisir cette valeur de a, il suffit de faire le calcul : a = T0/Z0. (On peut utiliser aussi le programme " Calcul " : voir ci-dessous).
Les autres paramètres par défaut de ce cadre correspondent à des valeurs moyennes dans la croûte continentale. On notera que la valeur de k est calculée automatiquement en fonction de celle de k, lorsque le petit carré blanc est coché ; en effet k = k / r .Cp. Cp est la capacité calorifique. Il s’agit de la quantité de chaleur nécessaire pour augmenter la température d’un corps donné de 1°. Dans le cas présent, on a choisi une valeur moyenne pour les matériaux de la croûte continentale de 1000 J / kg .° pour Cp et 2 700 kg / m3 pour r. Les données de ce cadre " Paramètres " sont utilisées pour les programmes " Graphe " et " Calcul ", qui sont eux-mêmes indépendants l’un de l’autre.
Le cadre " Calcul " permet de calculer (en cliquant sur le bouton " Calcul "), la température T (en °C), la profondeur Z (en km) et la P en (Kb) d’une roche à un temps t donné (en millions d’années = Ma), situé à une profondeur initiale Z0 (définie dans le cadre " Paramètres ") et se déplacent avec une vitesse u (définie dans le cadre " Calcul "). u est positif dans le cas de l’exhumation, négatif dans le cas de l’enfouissement (ou l’épaississement) ; elle est exprimée en mm/an ou, ce qui revient au même, en km/Ma. P est liée à Z par la relation simplifiée P = r g z (avec r , masse volumique des roches et g, accélération de la pesanteur = 9.81m/s2).
Dans le cadre " Graphe ", sont données les informations supplémentaires pour l’élaboration du graphe. " t max en Ma " est la durée de la simulation, en millions d’années (Ma). Dans le cas de la modélisation d’un enfouissement, " t max " donne la profondeur z maximale atteinte (z = z0 - ut, avec, dans ce cas, z0 = 0 et u négatif ; voir par ex. II et V).
" u en mm/an ", (ou km/Ma) donne les valeurs de la vitesse, positive dans le cas de l’exhumation, négative dans le cas de l’enfouissement (ou épaississement). Lorsque le petit carré blanc intitulé " simple " n’est pas coché, deux valeurs sont données (la vitesse maximale sera toujours portée dans la case de droite) : le programme trace alors 10 trajets PTt entre ces 2 valeurs extrêmes. On peut également tracer une seule courbe à la fois en sélectionnant le petit carré blanc sous u et en indiquant la valeur souhaitée.
" Z min-max " (en km), " T min-max " (en °C) donnent les dimensions du diagramme PT.
Le " Géotherme ", exprimé en Ma, donne l’équidistance des courbes " géothermes " rouges tracées lorsqu’on lance le programme " Graphe " avec une valeur u min. et une valeur u max. Dans le cas d’une valeur unique de u, Géotherme indique l’équidistance des repères sur le trajet PTt. Le petit carré blanc " Montre les Géothermes ", lorsqu’il est coché, montre les courbes " géothermes " si l’on a lancé le programme " Graphe " avec une valeur u min. et une valeur u max.
En haut, à droite de ce cadre, un petit carré blanc " Fond " permet de sélectionner ou non un " fond d’écran " montrant les faciès et gradients métamorphiques (voir ci-dessous). Deux petits carrés de couleur permettent de choisir la couleur des trajets PTt (carré du haut) et des géothermes (carré du bas). L’épaisseur du trajet peut également être modifiée.
La série de boutons : lance, respectivement, les programmes " Calcul ", " Graphe ". Le bouton " Ajout " permet de dessiner un nouveau trajet après modification d’un ou plusieurs paramètres (du cadre " Paramètres " et/ou du cadre " Graphe "), tout en conservant le (ou les) tracé(s) précédent(s). " Montre/Cache " permet de voir/cacher à nouveau le diagramme précédent que l’on a fermé/ouvert, sans relancer un nouveau tracé, pourvu que l’on n’ait pas cliqué sur le bouton " Efface " qui supprime les diagrammes précédents. On quitte le programme en cliquant sur le bouton " Fin ".
Un Menu Fichier contient les fonctions suivantes :
Lire Faciès :
Permet de changer le fichier (*.bmp) de fond d’écran, montrant, par ex., les domaines P-Z des différents faciès et réactions métamorphiques. Le carré blanc " Fond " du cadre " Graphe " doit être coché.
Efface Dernier Tracé :
Efface la dernière courbe, le dernier trajet PTt dessiné tout en conservant les courbes précédentes ; si l’opération est renouvelée plusieurs fois, on efface successivement les courbes précédentes
dans l’ordre inverse où elles ont été dessinées.
Rafraîchir Image :
Permet de réactualiser le graphe lorsque des informations erronées, héritées en général d’un tracé précédent sont conservées (par ex., diagramme de faciès que l’on veut faire apparaître ou disparaître). Il est indispensable de rafraîchir l’image lorsque l’on dessine un nouveau tracé (bouton " Ajout ") en ayant modifié les dimensions du graphe (Zmin-max du cadre Graphe).
Lire les paramètres (*.upl) :
Permet de lire les paramètres affichés dans un fichier *.UPL (tel que les exercices proposés et regroupés dans le sous-répertoire " exercices ").
Sauve les paramètres sous … :
Sauve tous les paramètres affichés dans la fenêtre principale dans un fichier UPL.
Sauve les paramètres (metamod.ini) :
Sauve tous les paramètres affichés dans la fenêtre principale (dans le fichier d’initialisation metamod.ini) pour une utilisation ultérieure du programme avec ces nouveaux paramètres au démarrage.
Fin : Ferme le programme.
Une aide rappelle les points essentiels pour l’utilisation de MetaMod et les objectifs des exercices. Grâce au sommaire, aux liens hypertextes et à l’index de l’aide, accédez à la rubrique de votre choix.
Remarque : avec les derniers systèmes d'exploitation de Windows, l'aide ne fonctionne plus. Rien de bien grave : Microsoft propose de se rendre sur cette page et de sélectionner un petit programme de mise à jour à installer sur votre ordinateur. L'aide fonctionne à nouveau.
La fenêtre du diagramme Z - T :
![]()
Le diagramme PT ou, pour être plus exact, Z-T est obtenu en cliquant sur le bouton " Graphe ". Ce diagramme peut être déplacé en cliquant, avec la souris, sur la barre bleue (en haut) et en faisant glisser la souris. Il peut être également redimensionné en tirant sur les arêtes ou les coins ou encore, en double-cliquant sur la barre bleue (plein écran). On note que Z augmente vers le bas. Le(s) trajet(s) PTt apparaissent en bleu (couleur par défaut), avec des tirets ou des cercles équidistants, en fonction de la valeur de " Géotherme " de la fenêtre principale. Si le graphe a été tracé avec " u " multiple, les géothermes apparaissent (en rouge, couleur par défaut).
Une fenêtre intitulée " Coordonnées " :

permet d’obtenir les coordonnées Z et T de n’importe quel point du diagramme Z-T en cliquant avec la souris. En cliquant sur les repères sur un trajet (ou à l’intersection des trajets et des géothermes s’ils existent), on obtient, en plus, le paramètre temps (en Ma, avec t=0 au début du trajet) et la vitesse u. Cette fenêtre peut être déplacée :
cliquer, avec la souris, sur la barre bleue et faire glisser. Les petits signes sur la barre bleue permettent de réduire cette fenêtre ou bien de fermer le diagramme Z-T.
En double-cliquant sur le diagramme, on revient à la fenêtre principale du programme.
La fermeture de la fenêtre " Graphe " n’efface pas le travail tant que l’on ne clique pas sur le bouton " Efface " et que l’on ne ferme pas le programme.
La fenêtre " Graphe " comporte trois menus :
Menu Fichier :
Lire Image : Permet de lire un diagramme Z - T conservé dans fichier *.bmp. Cette image est " passive " par rapport au programme : elle ne peut pas être redimensionnée, les courbes ne peuvent pas être effacer, etc.
Sauver Image sous : Permet de sauvegarder un diagramme Z - T dans fichier *.bmp. Noter que les étiquettes ne sont pas conservées.
Imprimer : Permet d’imprimer le graphe édité. Toutefois, sous Windows 311, le fond d’écran n’est pas (ou mal) imprimé. Si l’on souhaite imprimer une figure complète, faire une " impression d’écran " (bouton en haut à droite du clavier) que l’on imprime à partir d’un logiciel de dessin, de traitement d’images ou simplement de traitement de textes.
Lire faciès : Permet de changer le fichier (*.bmp) de fond d’écran, montrant, par ex., les domaines P-Z des différents faciès et gradients métamorphiques.
Efface Dernier Tracé : Efface la dernière courbe, le dernier trajet PTt dessiné tout en conservant les courbes précédentes ; si l’opération est renouvelée plusieurs fois, on efface successivement les courbes précédentes dans l’ordre inverse où elles ont été dessinées.
Rafraîchir Image : Permet de réactualiser le graphe lorsque des informations erronées, héritées en général d’un tracé précédent sont conservées (par ex., diagramme de faciès que l’on veut faire apparaître ou disparaître). Il est indispensable de rafraîchir l’image lorsque l’on dessine un nouveau tracé (bouton " Ajout ") en ayant modifié les dimensions du graphe (Z ou Tmin-max du cadre Graphe).
Cache Graphe : Cache momentanément le diagramme pour revenir à la fenêtre principale. Celui-ci n’est pas supprimé : le bouton Montre (ou Ajout) de la fenêtre principale le fait réapparaître non modifié (ou avec un tracé supplémentaire). Le graphe peut être également caché en double-cliquant sur l’écran (sauf sur une étiquette) ou en cliquant sur le coin en haut à droite du diagramme.
Menu Options :

Couleur Géothermes : Change la couleur des courbes géothermes, dans le cas d’un tracé à vitesses u variables.
Couleur du Tracé : Propose un choix de couleurs pour tracer les prochaines courbes.
Menu flottant (accessible en cliquant sur le graphe avec le bouton droit de la souris)

Voir fenêtre principale : fait apparaître la fenêtre principale au premier plan.
Nouvelle Etiquette : Permet d’écrire une information sur le diagramme. Sous Windows 95 (98 et NT), l’étiquette sera localisée là où l’on a fait apparaître le menu flottant. Taper le texte et valider en tapant sur la touche " entrée " du clavier. On peut choisir une autre place pour l’étiquette si, avant de valider, on clique ailleurs avec le bouton gauche de la souris. Sous Windows 311, cette dernière opération est absolument nécessaire.
Si l’on souhaite la supprimer, cliquer sur l’étiquette. Taper sur " oui " du message de confirmation.
Imprimer : Permet d’imprimer le graphe édité. Toutefois, sous Windows 311, le fond d’écran n’est pas (ou mal) imprimé. Si l’on souhaite imprimer une figure complète, faire une " impression d’écran " (bouton en haut à droite du clavier) que l’on imprime à partir d’un logiciel de dessin, de traitement d’images ou simplement de traitement de textes.
Lire faciès : Permet de changer le fichier (*.bmp) de fond d’écran, montrant, par ex., les domaines P-Z des différents faciès métamorphiques.
Efface dernier Tracé : Efface la dernière courbe, le dernier trajet PTt dessiné tout en conservant les courbes précédentes ; si l’opération est renouvelée plusieurs fois, on efface successivement les courbes précédentes dans l’ordre inverse où elles ont été dessinées.
Rafraîchir Image : Permet de réactualiser le graphe lorsque des informations erronées, héritées en général d’un tracé précédent sont conservées (par ex., diagramme de faciès que l’on veut faire apparaître ou disparaître). Il est indispensable de rafraîchir l’image lorsque l’on dessine un nouveau tracé (bouton " Ajout ") en ayant modifié les dimensions du graphe (Z ou T min-max du cadre Graphe).
Options:
Fond visible : Fait apparaître ou disparaître le dessin en fond d’écran (diagrammes des différents faciès métamorphiques par ex.).
Couleur du graphe : Propose un choix de couleurs pour tracer les prochaines courbes.
Couleur des géothermes : Change la couleur des courbes géothermes, dans le cas d’un tracé à vitesses u variables.
Cercles sur géothermes : Remplace les cercles, repères temporels sur le tracé, par un petit trait et réciproquement.
Le " fond d’écran " est un diagramme PT sur lequel sont portés les différents faciès métamorphiques, le géotherme moyen dans la lithosphère continentale et les principaux gradients métamorphiques rencontrés dans les chaînes de montagnes (hautes pressions - basses températures : HP-BT, Pressions intermédiaires - hautes températures : PI - HT et hautes températures - basses pressions : HT - BP). Le fichier " Facies.bmp " (Facies31.bmp pour windows 311) est utilisé par défaut. D’autres fichiers sont disponibles en utilisant les commandes " Lire faciès " : F.bmp, Ride.bmp (montrant les principaux faciès dans le manteau supérieur), Reaction.bmp (et Reac311.bmp ; montrant les champs de stabilité des principaux minéraux des métapélites). Selon la configuration de votre écran (16, 256 ou 65 536 couleurs), ces figures seront plus ou moins lisibles. Il est possible d’utiliser de nouveaux fichiers (au format *.bmp) préalablement copier dans le répertoire " metamod ". Lorsque de tels nouveaux fichiers sont appelés, une fenêtre demande les coordonnées en pixels de l’origine des axes, l’abscisse du point Z = 0 et T = 1200°C et l’ordonnée du point Z = 70km et T = 0°C (voir annexe III). On peut choisir de faire apparaître ou non ce fond d’écran sur le Graphe Z - T.
Les commandes classiques de Windows : Alt + lettre soulignée évite l’utilisation de la souris ; Tab sélectionne le paramètre ou bouton suivant ; Tab + Shift autorise la même opération en sens inverse. La barre d’espace permet d’activer les boutons et petits carrés lorsqu’ils sont sélectionnés.
QUELQUES EXERCICES DE SIMULATION DES
TRAJETS P - T - t :
![]()
Le logiciel propose quelques exercices pour lesquels les paramètres (et le fond d’écran) sont prédéfinis. Ils vont nous permettre de comprendre ce dont témoignent les évolutions des roches métamorphiques. Ils permettent de se familiariser avec le programme et peuvent ensuite être adaptés. Chacun exercice contient plusieurs fichiers (*.upl). Pour chercher un exercice dans le sous répertoire " exercices ", sélectionner la commande " Lire les paramètres " du Menu Fichier de la fenêtre principale. Dans la fenêtre " Ouverture " qui apparaît, ouvrir le répertoire " exercices ". Choisir parmi les six sous-répertoires qui sont proposés et l’ouvrir (par ex. : 1-paramètres). Ouvrir le premier fichier .UPL proposé (par ex. : 1a.upl). Les paramètres de la fenêtre principale du programme sont réactualisés. Lancer le bouton " Graphe " et renouveler l’opération avec les autres fichiers *.upl du sous - répertoire (sans effacer, en principe, le précédent tracé ; bouton " Ajout "). Chaque fichier *.upl correspond à un seul tracé. (Remarque : par mesure de précaution, ces fichiers sont protégés en écriture). Il est possible de modifier un fichier *.upl ou d’en créer de nouveaux en utilisant " Sauve les paramètres sous … "

Sur la figure 1, l’évolution thermique d’une roche dessine une boucle. Nous avons noté que les roches métamorphiques retenaient principalement le témoignage du pic en T. En conséquence, ce qui sera le mieux préservé dans ces roches est leur histoire rétrograde, c’est à dire l’exhumation, lorsqu’elles remontent vers la surface où elles affleurent. Les témoignages de l’histoire prograde, lorsque les roches s’enfoncent, au cours de l’épaississement, sont exceptionnels. Aussi, les modèles thermiques s’intéressent surtout à cette remontée .
I - Influence des paramètres
thermiques des roches sur la forme des trajets PTt :
![]()
Dans ce premier exercice, nous nous proposons de comprendre pourquoi les roches continuent de se réchauffer, dépassant le géotherme moyen, en remontant vers la surface pendant l ’amincissement d’une croûte continentale épaisssie(fig. 1b). Pour cela, nous allons simuler la trajectoire rétrograde, vers la surface, d’une roche portée à 45km de profondeur dans une chaîne de montagnes (2ème étape de la fig. 1a). Les conditions de T et Z initiales choisies (675°C et 45km) sont celles de nombreuses éclogites du Massif Central français. Mais ce choix est arbitraire.
Cet important réchauffement au cours de la remontée est fonction de la production de chaleur A des roches de la croûte et de la capacité qu’a cette croûte de diffuser la chaleur, quantifiée par k et k (conductivité et diffusivité thermiques). Ces paramètres n’ont pas des valeurs homogènes. A est grand dans la partie supérieure de la croûte continentale, faible dans la partie inférieure de la croûte continentale et dans la croûte océanique et très faible dans le manteau supérieur. Les valeurs de k (et k) dépendent des roches et de P et T (voir annexe). C’est l’influence de ces paramètres A, k et k que nous allons tester. La vitesse de remontée (u = 0.3 mm/an) est constante dans tout l’exercice.
a - Influence de la production de chaleur A : Avec "Lire les paramètres " du Menu Fichier, sélectionner exercices/1-paramètres/1a.upl. La vitesse de remontée u est de 0.3 mm/an (= 0.3 km/Ma). Les valeurs de A et de k sont des valeurs moyennes dans la croûte continentale. Clique sur le bouton " Graphe ". Le graphe noir qui se dessine correspond au trajet PTt rétrograde d’un échantillon porté à 45 km (et T = 675°C). Au cours de son exhumation, la roche se réchauffe dans un premier temps, avant de se refroidir. Grâce à la fonction " Nouvelle Etiquette " du Menu flottant, on aura soin d’indiquer pour chaque courbe les valeurs des paramètres.
Quittons le graphe et modifions la valeur de A sans changer k et u. Pour cela, sélectionner exercices/1-paramètres/1b.upl. La production de chaleur A est de 0 mW/ m3. Relancer " Graphe " sans cliquer " Efface ". On remarque que le nouveau trajet ne montre pas, cette fois, de réchauffement.
Prendre maintenant A = 0.8 mW/ m3, (Sélectionner exercices/1-paramètres/1c.upl.) valeur moyenne dans la croûte continentale supérieure. L’augmentation de T est importante et le DT entre les valeurs extrêmes de A est de plus de 200°.
b - Influence de la conductivité et la diffusivité thermiques (sélectionner exercices/1-paramètres/1d et 1e.upl) : sans effacer les graphes précédents, testons différentes valeurs de k (1.5 et 4 W/m°K et respectivement 6.10-7 et 15.10-7 m2/s pour k, calculé automatiquement ) avec, à nouveau, A=0.5 mW/ m3. Relancer " Graphe ". Plus k (et k) est grand, plus le pic de T est faible. Plus les roches sont conductrices de la chaleur, plus celle ci diffusera.
La forme du trajet PTt rétrograde, avec un réchauffement au début de la remontée, s’explique par le fait que les roches sont sources de chaleur (essentiellement radioactives) et que ces matériaux sont de mauvais conducteurs de la chaleur. A et k ont des effets inverses.
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale, sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires " exercices et 1-paramètres " : 1a.upl : trajet rétrograde avec les valeurs moyennes dans la croûte (A = 0.5 mW/ m3 et k = 2.5 W/m°K ) 1b et 1c.upl : idem en modifiant seulement la valeur
de A (A = 0 et 0.8 mW/ m3). |
I bis - Influence des sources de chaleur
A dans une croûte continentale épaissie ... :
![]()
Nous pouvons également appréhender l’influence de la production de chaleur A en suivant l’évolution du géotherme dans une croûte épaissie (fig. 1a). Effacer le graphe précédent s’il y a lieu, sélectionner exercices et 1-paramètres/1f.upl et lancer le programme en cliquant sur le bouton " Graphe ". Les lignes rouges sur la figure sont des portions de paraboles. Celles ci sont les géothermes depuis le temps 10 (courbe rouge la plus à gauche ), jusqu’à 220 Ma, avec une fréquence de 10 Ma. On peut lire l’âge de ces géothermes dans la fenêtre " Coordonnées " en cliquant aux intersections entre les courbes bleues et rouges. On constate que le géotherme se déplace, avec le temps, vers les hautes T.
Lorsque la croûte continentale s’épaissit, la source de chaleur radioactive (qui a une production de chaleur A) augmente. La croûte va donc se réchauffer lentement par conduction. On parle de relaxation thermique.... et influence de la vitesse de remontée :
Les 10 courbes bleus montrent les trajets rétrogrades d’une roche R de la figure 1 obtenus avec des vitesses d’exhumation variables : 0.1 mm/an, 0.2, ... 1mm/an. Plus la vitesse d’exhumation est grande (1 mm/an), moins le réchauffement est important. Lorsque la vitesse est grande, le mode de transfert de chaleur par convection devient dominant.
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale, sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires " exercices et 1-paramètres " et choisir 1f.upl |
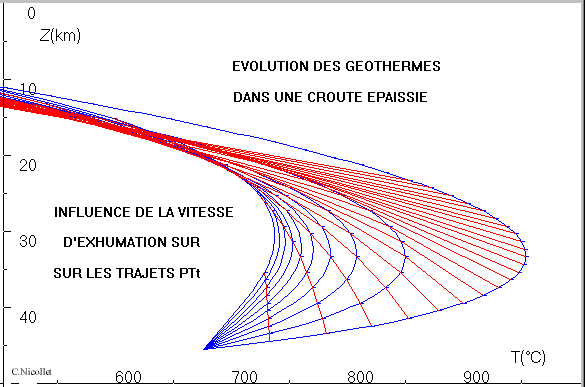
II - Le trajet prograde -
Influence de la vitesse d’enfouissement :
![]()
Bien que les roches métamorphiques n’enregistrent pas (ou peu) le trajet prograde (1ère étape de la fig. 1a), correspondant à l’enfoncement, au stade " épaississement ", il est possible de simuler cette étape. On va apprécier, dans cet exercice, l’influence de la vitesse d’enfoncement (ou de chevauchement) sur la forme du trajet prograde. On notera que la vitesse u est, ici, une vitesse verticale ; dans un chevauchement, u = V.sin a, avec a, angle du chevauchement et V, vitesse du chevauchement.

Trois graphes sont dessinés successivement, avec des vitesses u = -1 mm/an, puis -5 et -10 mm/an. " Z0 " est de 0km ; " t maxi " est fixé à 50, 10 et 5 Ma pour chaque graphe pour atteindre la profondeur de 50km ; on choisit des valeurs moyennes dans la croûte continentale pour A et k (exercices 2-enfouissement/2a, 2b, 2c.upl). Les trajets se déplacent vers les hautes pressions - basses températures lorsque la vitesse d’enfoncement u augmente. Pour les fortes valeurs de la vitesse (plusieurs cm/an) rencontrées dans les zones de subduction, le trajet coïncide ou est voisin du gradient de HP-BT visible sur le " fond d’écran ". Ce trajet traverse les faciès Schistes Bleus et Eclogite , effectivement rencontrés dans les zones de subduction. Pour les vitesses de l’ordre du mm/an, vitesse des chevauchements crustaux au cours d’une collision intracontinentale, il n’y a pas ou peu de perturbations thermiques : le trajet suit le géotherme moyen.
Si l’on augmente la conductivité k pour une vitesse donnée (par ex. 10mm/an : 2d.upl), on remarque que le trajet se déplace vers les hautes T d’une cinquantaine de degrés.
Le trajet devient de plus " haute pression - basse température " quand la vitesse d’enfoncement augmente : c’est l’influence prépondérante du facteur " convection " de l’équation de la chaleur. Si k est fort, les roches se rééquilibrent mieux avec l’environnement chaud dans lequel il se trouve.
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale, sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires exercices et 2-enfouissement : 2a., 2b., 2c.upl : u = -1, -5, -10 mm/an ; t max : 50, 10, 5 Ma A = 0.5 mW/ m3 et k = 2.5 W/m°K : valeurs moyennes dans la croûte 2d.upl : u = -10 mm/an et k = 4 W/m°K |
Remarque : On peut apprécier les limites de la modélisation en calculant (avec le bouton " Calcul " de la fenêtre principale) la température à 650km de profondeur (dans le cadre " Calcul ", fixer t à 650 Ma et u à -1mm/an). La température obtenue (5637°C) est largement surévaluée, puisque c’est la T qui règne dans le noyau. En réalité, la T à 650km, dans le manteau, est estimée à 1600°C. Le calcul ne prend pas en considération l’importante chute de la production de chaleur en passant de la croûte continentale (A=0.5 mW/ m3) au manteau (A=0.02 mW/ m3).
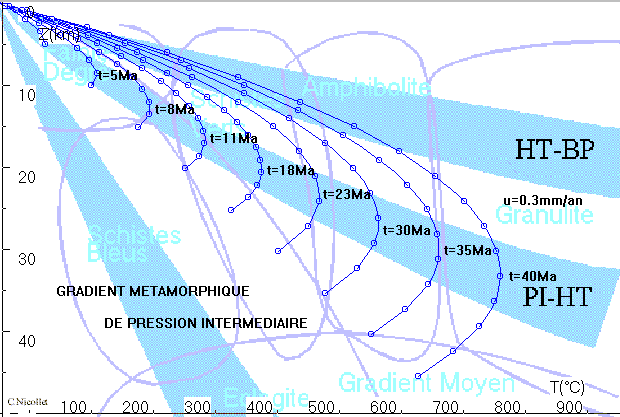
III - Le trajet rétrograde et le gradient
métamorphique de Pression intermédiaire :
![]()
Dans la chaîne paléozoïque hercynienne, bien représentée dans le Massif Central, le Massif Armoricain et Pyrénées, l’évolution métamorphique régionale d’une série de roches matérialise le plus souvent un " gradient métamorphique de type Pressions Intermédiaires " (barrovien). De rares échantillons d’éclogites peuvent témoigner de Pressions significativement plus élevées : elles vont servir dans cet exercice de valeurs maximales (Z0 = 45 km et T = 675°C).
Dans cet exercice, nous allons suivre les trajectoires d’exhumation (rétrogrades) d’échantillons enfoncés à différentes profondeurs, au cours d’une collision, et qui sont exhumés par le simple processus de remontée gravitaire (isostatie) associé à l’érosion (2ème étape de la fig. 1a). Les vitesses de remontée, dans un tel contexte géodynamique, sont évaluées entre 0.2 et 0.5 mm/an. Nous allons tracer les trajectoires rétrogrades d’une série d’échantillons à des profondeurs initiales de 45, 40, ... 5 km et remontant à une vitesse constante u = 0.3 mm/an. Pour cela, lancer " exercices 3-gradient/3a " avec Z0 = 45, puis diminuer Z0 de 5 en 5 jusqu’à 30km, ensuite opérer de même avec " 3b.upl ". On notera, pour chaque trajet, grâce à une étiquette, le temps auquel le pic en T a été atteint. On remarque que les pics des T coïncident avec le gradient de Pressions intermédiaires (PI - BT). D’autre part, ces pics de T ne sont pas atteints en même temps : le gradient métamorphique n’a jamais existé à un moment " t " donné de l’histoire de la chaîne.
Le régime thermique du gradient de PI est caractéristique d’une zone en collision dans laquelle l’épaississement de la croûte, suivi d’un amincissement par érosion, s’accompagne d’un réchauffement significatif, au-delà des conditions du géotherme moyen. Dans les Alpes, chaîne récente, ces conditions sont plus localisées (dans les Alpes dites penniques).
Les pics des T des différents échantillons, dont témoignent les paragenèses des roches métamorphiques, matérialisent un gradient métamorphique de PI (voir en première partie dans LES ROCHES METAMORPHIQUES : TEMOINS DE L’EVOLUTION THERMIQUE DE LA LITHOSPHERE - Gradient métamorphique et trajets P,T, t ...).
Quelles sont les paragenèses (associations minéralogiques) de roches ayant suivies de telles évolutions thermiques ? Elles dépendent, tout d’abord, de la nature des roches. Supposons qu’ils s’agissent de roches argileuses (= métapélites ou micaschistes). Utilisons en " fond d’écran ", un diagramme montrant les champs de stabilité de quelques minéraux importants trouvés dans ces roches ainsi que la courbe d’anatexie (A) marquant le domaine où les roches commencent à fondre. Pour cela, avec " Lire faciès ", sélectionner " Reaction.bmp " (sans effacer la figure réalisée jusque là). Les abréviations utilisées sur cette figure sont : Musc : muscovite ; Q : quartz ; Biot : biotite ; Gt : grenat ; Std : staurotide ; Cord : cordiérite ; Sill ou S : sillimanite ; Fk : feldspath potassique ; A : andalousite et courbe d’anatexie.
Les roches les plus superficielles (Z0 = 5, 10 et 15 km) n’atteignent pas la courbe qui limite le champ de stabilité de la muscovite (ce minéral est stable à droite de la première courbe). Cette courbe est recoupée deux fois par la roche Z0 = 20 km. La première fois, lorsque celle-ci se réchauffe : le minéral apparaît dans la roche. La deuxième fois, au cours du refroidissement, mais il ne se passe rien. En effet, nous avons expliqué précédemment qu’une roche métamorphique conserve l’association minéralogique de plus hautes températures. Le trajet P-T-t n’a pas atteint la courbe qui limite le domaine de stabilité de la biotite : la roche est un micaschiste à muscovite (quartz, chlorite, feldspath, minéraux accessoires peuvent être présents). Le trajet de la roche Z0 = 25 km franchit la réaction " Biot " : la roche est une métapélite à 2 micas (biotite et muscovite).
Appliquons le même raisonnement aux autres roches : la paragenèse d’une roche correspond aux minéraux stables au pic en température du trajet thermique de cette roche. Ainsi la roche à
- Z0 = 30 km est à muscovite, biotite , grenat, disthène (K), quartz,
- Z0 = 35 km est à muscovite, biotite , grenat, staurotide, disthène, quartz,
Le trajet de la roche Z0 = 40 km franchit la courbe de l’anatexie et commence à fondre : il s’agit d’une migmatite à sillimanite, (biotite, muscovite, grenat, quartz et felsdpath). La roche Z0 = 45 km est également une migmatite; mais elle ne contient plus de muscovite : en effet, ce minéral a disparu au cours de la réaction Musc + Q = Sill + Fk + H2O.

On peut illustrer ces paragenèses en utilisant les documents du paragraphe " Le tracé du gradient métamorphique du dôme du Lévezou " dans Nicollet C. et M. (1996, Bull. APBG, p.299-341)
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale, sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires exercices et 3-gradient : 3a.upl : u = 0.3 mm/an ; Z0 : 45km ; diminuer
Z0 de 5 en 5 km jusqu’à 30km puis En fin d’exercice, avec " Lire faciès ", choisir le fond d’écran " Reaction.bmp ". |
IV - Le gradient de Hautes Températures
- Basses Pressions :
![]()
Dans le Sud-est du Massif Central (Massif du Pilat, du Velay, Montagne Noire), dans les Pyrénées ..., le gradient métamorphique est du type Hautes Températures - Basses Pressions. Celui - ci se surimpose à un métamorphisme de PI. Ce métamorphisme de HT, tardif dans l’orogène hercynienne (320 – 280 Ma), est associé à des structures tectoniques en extension. Celles - ci témoignent de l’amincissement tardi orogénique qui a ramené rapidement la croûte à son épaisseur normale. Au cours de ce processus tectonique, la vitesse d’exhumation augmente significativement.
Dans un premier temps (exercice 4-exhumation/4a.upl), nous allons suivre le trajet d’un échantillon remontant à la vitesse de 0.3 mm/an, vitesse moyenne au cours de la rééquilibration gravitaire associée à l’érosion : le pic en T de ce trajet se place sur le gradient métamorphique de PI (voir exercice précédent).
Nous allons supposer, maintenant, qu’au pic en T, la vitesse d’exhumation augmente. A partir du pic en T, modifions la vitesse d’exhumation : 5 et 10 mm/an (exercices 4- exhumation /4 b et c.upl), vitesses typiques au cours de processus d’exhumation tectonique. Le pic en T est déplacé vers les Basses Pressions. Il se situe dans le domaine du gradient métamorphique de HT-BP. Si l’on reproduit cet exercice sur d’autres échantillons enfouis à des profondeurs variables, leurs pics en T matérialiseront un gradient de HT-BP.
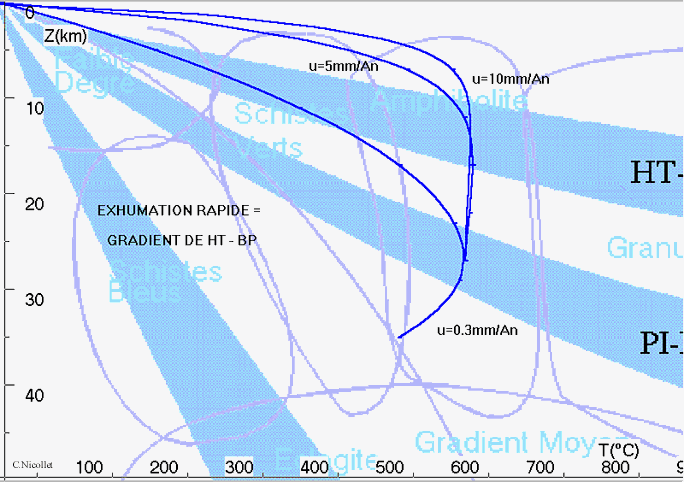
Comme dans l’exercice précédent, utiliser en fond d’écran le diagramme " Reaction.bmp ". La paragenèse (correspondant aux minéraux stables au pic en température du trajet thermique) d’une métapélite exhumée rapidement selon le trajet ci-dessus est à : muscovite, biotite , cordiérite, sillimanite (pour u = 5mm/an) ou andalousite (pour u =10 mm/an), quartz. Le grenat n’est plus stable.
En remontant rapidement, les roches n’ont pas le temps de se refroidir et arrivent chaudes à faible profondeur : " la convection " l’emporte sur la " conduction ".
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale,
sélectionner " Lire les paramètres ",
ouvrir successivement les sous-répertoires exercices et 4- exhumation: En fin d’exercice, avec " Lire faciès ", choisir le fond d’écran " Reaction.bmp ". |
V - Préservation des Schistes
Bleus et éclogites de basses températures :
![]()
Les roches de HP-BT, caractéristiques des faciès " Schistes Bleus " et " Eclogite de BT " (T< 500°C), bien représentées dans les convergences récentes (océan-océan, océan-continent ou continent - continent jeune : Alpes ; Queyras et Corse), deviennent rares dans les chaînes anciennes (paléozoïques et précambriennes ; dans la chaîne hercynienne de France, le faciès Schistes Bleus est connu à l’Ile de Groix et au Bois de Céné, Vendée). Pourquoi ? Remarquons, que dans les périodes très récentes (<10Ma), ces roches se forment dans les zones de convergence océan-océan (pourtour péri - pacifique), où les vitesses, très grandes dans les zones de subduction, sont les seules qui permettent d’atteindre des gradients d’aussi BT-HP (voir II). En conséquence, ce type de métamorphisme se forme dans la période précoce de l’histoire d’une chaîne, avant la collision continent - continent. D’autre part, la préservation de ces conditions dépend de l’évolution thermique des roches lors de leur remontée à la surface.
Dans la première étape de cet exercice, nous allons porter un échantillon à 50 km de profondeur, avec une vitesse de -10 mm/an (exercice 5-SB/5a.upl). A cette vitesse, la température reste faible à 50 km (voir II). Dans la deuxième étape, nous faisons remonter la roche à différentes vitesses, contrôlées par les processus d’érosion (par ex. : 0.25 et 1 mm/an : exercice 5-SB/5b et 5c.upl) et d’exhumation tectonique (10 mm/an : exercice 5-SB/5d.upl). On constate que pour les faibles vitesses, le trajet sort du domaine du faciès Schistes Bleus et que le pic en température se situe dans le faciès Schistes Verts : la paragenèse préservée sera donc du faciès Schistes Verts. Pour des vitesses rapides (>5mm/an), l’augmentation de la température lors du trajet rétrograde est trop faible (env. 15° avec u=10mm/an) pour que les roches recristallisent : les conditions de HP-BT du faciès Schistes Bleus – éclogites de BT sont préservées.

En conséquence, les conditions de HP-BT ne seront préservées que si les roches sont exhumées rapidement, c’est à dire précocement dans l’histoire de la chaîne. Mais, dans ce cas, celles-ci risquent d’être érodées rapidement. Par contre, si les roches restent à l’abri en profondeur et sont impliquées dans la collision, elles seront réchauffées et perdront la trace des conditions HP-BT. En conséquence, ces roches deviennent rares dans les chaînes anciennes.
|
Récapitulatif pour l’utilisation du programme : Dans le Menu Fichier de la fenêtre principale, sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires exercices et 5 - SB : 5a.upl : u = -10 mm/an ; Z0 : 0 km puis |
VI - Reliques de HP dans un gradient de MP dans le dôme lépontin (Alpes Centrales)
La partie Ouest de la carte métamorphique des Alpes de la CCGM fait apparaître distinctement deux domaines métamorphiques grâce à des couleurs bien contrastées : à l'ouest, un domaine aux couleurs bleu – violette, indiquant, selon le diagramme PT, un gradient de HP-BT, caractéristique du début de la collision, après subduction de l'océan alpin et sa marge. Dans les Alpes Centrales, le domaine Lépontin est facilement repérable sur cette carte avec ses couleurs rouge - orange - verte qui indiquent les conditions d'un gradient de MP-HT. La carte des isogrades et des limites d'apparition des minéraux montre une zonéographie caractéristique d'un gradient métamorphique de moyenne pression – haute température ( figure ) croissant du Nord, où les conditions sont anchimétamorphiques vers le Sud, où elles atteignent les domaines de stabilité de l'association sillimanite + feldspath potassique, c'est-à-dire au-delà des conditions de stabilité de l'assemblage muscovite + quartz. Les migmatites sont abondantes. Plus au Sud, la ligne insubrienne tronque brutalement le dôme Lépontin :
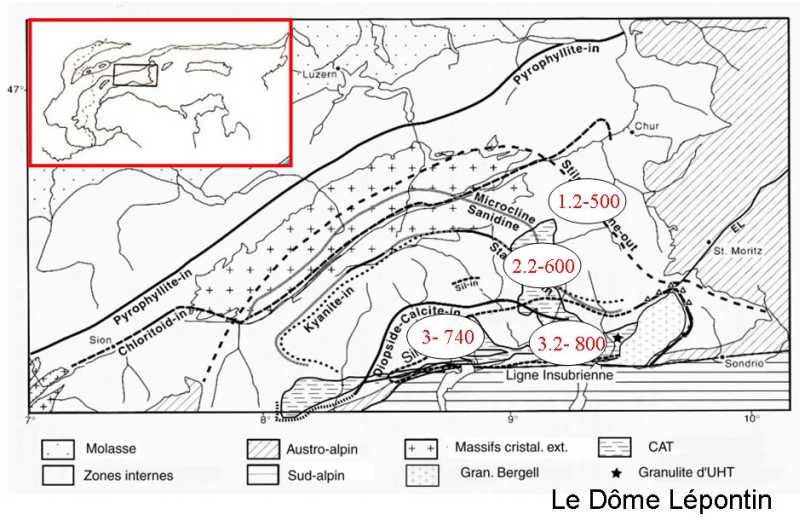
Cette carte (d'après Frey et Mählmann, 1999 et Engi et al, 2004) montre les isogrades ou limites d'apparition de quelques minéraux alumineux caractéristiques : stilpnomélane, chloritoïde, staurotide, disthène, et sillimanite – fibrolite caractéristique d'un gradient de MP-HT. Les conditions de PT de quelques reliques sont portées dans les ellipses en GPa et °C.
Le CAT, chenal d'accrétion tectonique, constitue un empilement de nappes qui contient des reliques d'éclogites et péridotites à grenat, indiquant des hautes à très hautes pressions. Notons, dans le CAT, à l'ouest du massif de Bergell, la présence de l'unique témoin phanérozoïque de métamorphisme d'ultra haute température, avec des paragenèses à saphirine, dans le complexe du Gruf (étoile). Ces témoins éclogitiques ont été différemment rétromorphosées dans les conditions du faciès Amphibolite, en fonction de la disponibilité des fluides et de la déformation. Un gradient métamorphique (précoce) discontinu de HP peut être tracé grâce aux reliques éclogitiques : il montre, comme le gradient de MP, une augmentation des conditions depuis le Nord, avec P=1-1,5 GPa à 500°C , vers le Sud avec P=3,3 GPa – 800- 900°C .
Le gradient du métamorphisme précoce de HP ainsi que celui du métamorphisme de moyenne pression sont, tous les deux, croissants depuis le Nord vers le Sud. L'exhumation a préservé la disposition initiale de la plaque plongeant en subduction vers le Sud. Les conditions éclogitiques sont datées dans un intervalle de temps de 55 à 35Ma ; le gradient de MP est daté à 32Ma, impliquant une exhumation rapide d'unités éclogitiques depuis les grandes profondeurs, supérieures à 100 km au Sud , jusqu'à des profondeurs modestes (15- 25 km ).
Dans cet exercice, nous allons suivre les trajets de ces reliques de HP exhumées à une vitesse moyenne de 3mm/an. On remarque que les pics en Température de ces trajets d'exhumation dessinent un gradient de MP-HT.
Notons que le trajet le plus « chaud » passe dans le domaine du métamorphisme d'UHT. Il est possible que les granulites d'UHT du complexe du Gruf aient suivi un tel trajet (roches continentales enfouies à grande profondeur), mais auraient perdu la mémoire de leur exhumation jusqu'au UHT.
|
Récapitulatif pour l'utilisation du programme : Sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires exercices et 6 - DomeLepontin : 6a à 6g.upl : u = 3 mm/an ; Z0 : variable |
VII - Genèse de la croûte océanique :
Quittons la lithosphère continentale pour nous intéresser à un site géodynamique de la lithosphère océanique où les déplacements verticaux sont importants et rapides : il s’agit de la ride océanique. Nous allons simuler la remontée, à des vitesses variées (exercice 7-Ride ), d’un échantillon de manteau situé à 130 km de profondeur ; il est, à cette profondeur, à plus de 1400 °C. Notons que le manteau supérieur, pauvre en éléments radioactifs, a une production de chaleur A proche de zéro. D’autre part, si le gradient géothermique (a) est très élevé au niveau de la ride, sa valeur diminue rapidement avec la profondeur.

On constate que pour de fortes vitesses d’exhumation (u = 10 mm/an), à la verticale de la ride, la température ne diminue significativement qu’à faibles profondeurs. Dans ce cas, la roche franchit le solidus du manteau et fond partiellement, produisant le magma à l’origine de la croûte océanique. Pour des vitesses variant entre 1 et 10 mm/an, la courbe pénètre de plus en plus au delà du solidus, impliquant des taux de fusion partielle du manteau de plus en plus importants. Ainsi, l’apport magmatique dans les rides à croissance lente est-il beaucoup plus faible quand dans les rides à croissance rapide.
A l’intérieur des cellules de convection, en s’éloignant de la verticale de la ride, les roches se déplacent à des vitesses plus faibles et subissent des transformations à l’état solide (= métamorphiques), sans fondre.
|
Récapitulatif pour l’utilisation du programme : Sélectionner " Lire les paramètres ", ouvrir successivement les sous-répertoires exercices et 7 - Ride : 7a, 7b et 7c.upl : u = 0.1, 1 et 10 mm/an ; Z0 : 130 km ; k = 3.5 W/m°K ; A = 0 mW/ m3 |
A l’intérieur des cellules de convection, les roches mantelliques qui remontent rapidement à la verticale des rides fondent partiellement, produisant le magma à l’origine de la croûte océanique. Cette production magmatique est plus faible dans les rides à croissance lente que dans celles à croissance rapide. A l’intérieur des cellulles de convection où les vitesses de déplacement sont faibles, les transformations se font à l’état solide (=métamorphiques).
I - Les variations de la production de chaleur (A) et de la conductivité thermique (k) dans la lithosphère continentale :
Le logiciel " MetaMod " suppose, pour chaque simulation, que A et k sont constants. Dans la nature, il n’en est pas de même. Ainsi, dans la lithosphère océanique, pauvre en éléments radioactifs, la production de chaleur A est bien plus faible que dans la lithosphère continentale. Dans la croûte continentale, la répartition verticale de ces éléments est inégale. Ainsi, A est supérieur à 1 mW/m3 jusqu'à 16km de profondeur, varie entre 0.3 et 0.7 mW/m3 jusqu'à la base de la croûte et n’est plus que de 0.02 mW/m3 dans le manteau supérieur. Ces valeurs nous permettent de comprendre pourquoi, lors d’un épaississement de la croûte continentale (fig. 1a), les géothermes dépassent le géotherme moyen (fig. 1b). Dans ce cas, on augmente l’épaisseur de la croûte (superficielle) qui a une production de chaleur A élevée.
La conductivité des roches k augmente avec la température, diminue avec la profondeur. Elle varie en fonction des roches. . Quoiqu’il en soit, d’une manière générale, les roches sont de mauvais conducteurs thermiques et leurs conductivités restent faibles, inférieures à 10 W/m°K. Dans la croûte continentale, k varie, en moyenne, entre 1.5 dans la croûte profonde et 3 W/m°K dans la croûte superficielle. La valeur moyenne de 2.5 W/m°K utilisée dans nos exercices est une valeur raisonnable. On prendra 3.5 W/m°K dans le manteau lithosphérique.
II - L’équation du géotherme :
Nous avons écrit plus haut que la dissipation de la chaleur à l’intérieur du globe est exprimée par l’équation de la propagation de la chaleur :
![]()
si l’on ne considère que les transferts verticaux (à la vitesse u), en fonction de la profondeur z. T est la température, t le temps, ![]() la masse volumique. Cp est la capacité thermique (mesure la chaleur nécessaire pour faire augmenter de un degré la température d’un volume unitaire de roche). A est la production de chaleur,
la masse volumique. Cp est la capacité thermique (mesure la chaleur nécessaire pour faire augmenter de un degré la température d’un volume unitaire de roche). A est la production de chaleur, ![]() (kappa) la diffusivité thermique, c’est à dire de la capacité de ces roches à laisser circuler la chaleur. Cette équation fait apparaître les principaux modes de transfert de chaleur (second terme de l’équation : transfert de chaleur par conduction ; troisième terme de l’équation : transfert de chaleur par convection) et de production (ou pertes) de chaleur (premier terme de l’équation).
(kappa) la diffusivité thermique, c’est à dire de la capacité de ces roches à laisser circuler la chaleur. Cette équation fait apparaître les principaux modes de transfert de chaleur (second terme de l’équation : transfert de chaleur par conduction ; troisième terme de l’équation : transfert de chaleur par convection) et de production (ou pertes) de chaleur (premier terme de l’équation).
Dans les Zones instables de la lithosphère : Nous avons remarqué que le signe - devant le troisième terme de l’équation indique une compétition entre les termes convectif et conductif. Si le terme convectif est grand (c’est à dire si u, la vitesse, est grande) devant le terme conductif, la température varie peu en fonction du temps et par voie de conséquence, de la profondeur. A la limite des plaques lithosphériques, zones de subduction et rides océaniques, les vitesses de déplacement sont grandes (u <0 dans le premier cas et >0 dans le deuxième cas). En conséquence, la température varie peu en fonction de la profondeur : les isothermes sont étirés dans les zones de subduction et resserrés au niveau des rides océaniques.
Dans les Zones stables : A l’intérieur d’une plaque lithosphérique, les déplacements verticaux et la variation de T en fonction du temps (![]() ) sont proches de 0. L’équation de chaleur se simplifie de la sorte :
) sont proches de 0. L’équation de chaleur se simplifie de la sorte :

Ceci est l’équation de Poisson dont la solution est l’équation d’une parabole :
![]()
Q0 et T0 sont respectivement, le flux de chaleur à la surface du sol (quantité de chaleur qui traverse une surface en un temps donné) et la T à la surface. Ceci est l’équation du géotherme dans la partie lithosphérique à l’intérieur d’une plaque stable où le transfert de la chaleur est essentiellement conductif. Par contre, dans le manteau sous-jacent à cette lithosphère, le transfert est convectif. Au delà de 250km, le géotherme devient essentiellement linéaire avec un gradient de l’ordre de 0.4°C/km.
On peut calculer des géothermes dont les formes varient en fonction de Q0, k et A. En effet, la valeur de ces paramètres varie significativement en fonction de la nature des roches (voir ci-dessus).
III - Création d’un nouveau " fond d’écran " (fichier *.bmp) :
Le logiciel est fourni avec plusieurs diagrammes P T, dits " Fond d’écran ", qui montrent les principaux faciès et gradients métamorphiques et géotherme moyen. Pour passer d’une figure à l’autre, il suffit d’utiliser la commande " Lire Faciès ", accessible à partir des différents menus et de choisir parmi les fichiers *.bmp proposés.
De plus, le logiciel donne la possibilité de personnaliser son " fond d’écran ". Pour cela, copier dans le répertoire " METAMOD " la figure souhaitée, en format bipmap (*.bmp). Utiliser la commande " Lire Faciès " et choisir le nouveau fichier : une fenêtre vous informe que le fichier metamod.ini ne possède pas les paramètres de ce nouveau fichier.
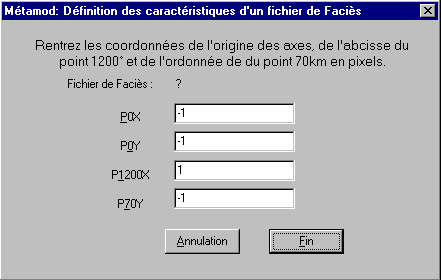
En cliquant sur " OK ", une nouvelle fenêtre propose de rentrer les coordonnées, en pixels, de l’origine des axes, de l’abscisse du point T = 1200°C (et Z = 0 km) et l’ordonnée du point Z = 70km (et T = 0°C).
Une fois ces informations données, cliquer " Fin " et le nouveau fond d’écran est connu de " METAMOD ". La commande " Annulation " nous ramène au fond d’écran préalablement utilisé.
En cas d’erreur sur les coordonnées d’un fichier *.bmp, éditer le fichier " metamod.ini " du répertoire " Metamod " (avec un quelconque éditeur de texte, par ex. Notepad) et modifier directement les valeurs présentées sous cette forme :
Nom du fichier : [ride]
Abscisse du point 0 : P0X=0
Ordonnée du point 0 : P0Y=40
Abscisse du point 1200°C : P1200X=250
Ordonnée du
point 70 km : P70Y=180
Remarque : Les valeurs de 1200°C et 70 km ne constituent nullement des limites aux dimensions du fichier " fond d’écran " !
IV - Base mathématique du logiciel METAMOD :
Le programme utilisé dans cet exercice est basé sur une solution analytique de l’équation de la chaleur (2), proposée par Carslaw et Jaeger en 1959. Celle-ci est :
T = az + kAt/k
+aut + 1/2(a+kA/uk)
{(z-ut)e-uz/k
erfc[(z-ut)/2![]() ]-(z+ut) erfc[(z+ut)/2
]-(z+ut) erfc[(z+ut)/2![]() ]} (3)
]} (3)
k est la conductivité thermique, (liée
à ![]() , la diffusivité thermique, par
, la diffusivité thermique, par
![]() ) et a
la pente initiale (= gradient géothermique
) et a
la pente initiale (= gradient géothermique ![]() )
du géotherme ; erfc () est une fonction d’erreur. La vitesse de
déplacement (u) est constante, de telle manière que la profondeur
z à un temps t est z(t) = z0 - ut.
)
du géotherme ; erfc () est une fonction d’erreur. La vitesse de
déplacement (u) est constante, de telle manière que la profondeur
z à un temps t est z(t) = z0 - ut.
V - Adresse utile : Si vous avez des problèmes avec METAMOD, des commentaires ou des suggestions, n’hésitez à me contacter :
Prof. Christian Nicollet
Université Clermont Auvergne
e-mail :
__________________________